Projects Thingys You Need to Know How Objects Drop at the Same Speed

Do falling objects driblet at the same rate (for instance a pen and a bowling brawl dropped from the same peak) or do they driblet at different rates? I know a feather floats downwardly very slowly but I would think a heavy object would fall faster than a calorie-free object. Thank you for your help. I take a bet on this ane.

Asked by: Terri

Respond

If no air resistance is present, the rate of descent depends only on how far the object has fallen, no matter how heavy the object is. This means that ii objects will reach the ground at the same time if they are dropped simultaneously from the same acme. This argument follows from the police of conservation of energy and has been demonstrated experimentally by dropping a feather and a atomic number 82 ball in an airless tube.

When air resistance plays a role, the shape of the object becomes important. In air, a feather and a brawl practise not autumn at the aforementioned charge per unit. In the case of a pen and a bowling ball air resistance is small compared to the force a gravity that pulls them to the ground. Therefore, if yous drop a pen and a bowling brawl you could probably non tell which of the two reached the basis first unless you dropped them from a very very high tower.
Answered by: Dr. Michael Ewart, Researcher at the University of Southern California

The above answer is perfectly right, simply, this is a question that confuses many people, and they are hardly satisfied past us self-assured physcists' answers. There is one good explanation which makes everybody content -- which does not belong to me, but to some famous scientist simply I tin can't remember whom (Galileo?); and I think it would be good to accept it upward here.

(The argument has nothing to do with air resistance, information technology is assumed to be absent-minded. The answer by Dr. Michael Ewart answers that part already.)

The argument goes as follows: Assume we take a 10kg ball and a 1kg ball. Permit us presume the 10kg brawl falls faster than the 1kg ball, since it is heavier. Now, lets necktie the two assurance together. What will happen and so? Volition the combined object fall slower, since the 1kg ball will hold back the 10kg brawl? Or volition the combination autumn faster, since it is now an 11kg object? Since both can't happen, the only possibility is that they were falling at the aforementioned rate in the beginning place.

Sounds extremely convincing. But, I think at that place is a slight fallacy in the argument. It mentions nix near the nature of the forcefulness involved, so it looks like information technology should work with whatever kind of strength! However, it is not quite truthful. If we lived on a world where the 'falling' was due to electrical forces, and objects had masses and permanent charges, things would exist different. Things with zero charge would non fall no affair what their mass is. In fact, the falling rate would exist proportional to q/m, where q is the charge and thousand is the mass. When you tie two objects, one and two, with charges q₁, q₂, and m_ane, m₂, the combined object will fall at a rate (q₁+q₂)/(m₁+m_two). Assuming q₁/thousand₁ < q₂/m_ii, or object two falls faster than object ane, the combined object will fall at an intermediate rate (this can be shown easily). Merely, there is some other point. The 'weight' of an object is the force acting on it. That is merely proportional to q, the accuse. Since what matters for the falling rate is q/m, the weight will have no definite relation to rate of fall. In fact, you could have a aught-mass object with charge q, which will fall infinitely fast, or an space-mass object with charge q, which will not fall at all, but they will 'counterbalance' the same! So, in fact, the original argument should be reduced to the post-obit statement, which is more accurate:

If all objects which have equal weight autumn at the same charge per unit, and so _all_ objects volition fall at the same charge per unit, regardless of their weight.

In mathematical terms, this is equivalent to saying that if q_i=q₂ then m₁=m₂ or, q/m is the aforementioned for all objects, they volition all fall at the same rate! All in all, this is pretty hollow an argument.

Going back to the case of gravity.. The gravitational strength is

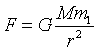
( G is a abiding, called abiding of gravitation, Yard is the mass of the attracting body (here, earth), and thousand₁ is the 'gravitational mass' of the object.)

And newton'southward police force of motion is

where m_ii is the 'inertial mass' of the object, and a is the acceleration.

Now, solving for dispatch, nosotros observe:

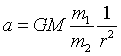
Which is proportional to m_one/m_two, i.e. the gravitational mass divided past the inertial mass. This is our old 'q/yard' from the electrical case! At present, if and only if chiliad₁/m₂ is a constant for all objects, (this constant tin exist absorbed into Grand, so the question tin can exist reduced to thousand₁=m₂ for all objects) they will all autumn at the aforementioned rate. If this ratio varies, then we will have no definite relation between rate of autumn, and weight.

And then, all in all, we are back to square one. Which is just canceling the masses in the equations, thus showing that they must autumn at the same rate. The equality of the ii masses is a necessity for full general relativity, and enters it naturally. As well, the two masses have been found to be equal to extremely good precision experimentally. The correct answer to the question 'why objects with different masses fall at the same rate?' is, 'beacuse the gravitational and inertial masses are equal for all objects.'

And so, why does the argument sound and so convincing? Since our daily feel and intuition dictates that things which weigh the same, fall at the same rate. One time we assume that, we have implicitly already causeless that the gravitational mass is equal to the inertial mass. (Wow, what things we do without noticing!). The rest of the argument follows hands and naturally...
Answered by: Yasar Safkan, Physics Ph.D. Candidate, G.I.T.

coxmencre1945.blogspot.com

Source: https://www.physlink.com/education/askexperts/ae6.cfm

Share this post